はじめに †
確率統計の教科書を眺めていて、z検定は母分散が既知である必要があり、t検定は母分散が未知である必要があるとの記述を発見。 ではz検定の性能とt検定の性能を比較するとどんなもんなんだろうと疑問を持ったのでシミュレーションを回してみました。
z検定で母分散が未知 †
z検定は母分散が未知である時に使うものですが、標本分散を放り込んでみたらどうなるのかなと思って書いてみました。
from scipy.stats import norm
import numpy
def z_test_unknown(N):
M = 100000
count = 0
for i in range(M):
X = numpy.array(norm.rvs(0, 1, N))
avg = X.mean()
std = X.std()
z = avg / (std / numpy.sqrt(N))
p = norm.cdf(- numpy.abs(z), 0, 1) * 2
if(p < 0.05):
count += 1
print("error rate," + str(N) + "," + str(float(count) / float(M)))
for i in [2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100,
110, 120, 130, 140, 150, 160, 170, 180, 190, 200]:
z_test_unknown(i)
z検定で母分散が既知 †
from scipy.stats import norm
import numpy
def z_test_known(N):
M = 100000
count = 0
for i in range(M):
X = numpy.array(norm.rvs(0, 1, N))
avg = X.mean()
std = X.std()
z = avg / (1.0 / numpy.sqrt(N))
p = norm.cdf(- numpy.abs(z), 0, 1) * 2
if(p < 0.05):
count += 1
print("error rate," + str(N) + "," + str(float(count) / float(M)))
for i in [2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100,
110, 120, 130, 140, 150, 160, 170, 180, 190, 200]:
z_test_known(i)
t検定で母分散が未知 †
from scipy.stats import norm
from scipy.stats import t
import numpy
def t_test(N):
M = 100000
count = 0
for i in range(M):
X = numpy.array(norm.rvs(0, 1, N))
avg = X.mean()
std = X.std()
t = avg / (std / numpy.sqrt(N - 1))
p = t.cdf(- numpy.abs(t), df = N - 1) * 2
if(p < 0.05):
count += 1
print("error rate," + str(N) + "," + str(float(count) / float(M)))
for i in [2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100,
110, 120, 130, 140, 150, 160, 170, 180, 190, 200]:
t_test(i)
解説 †
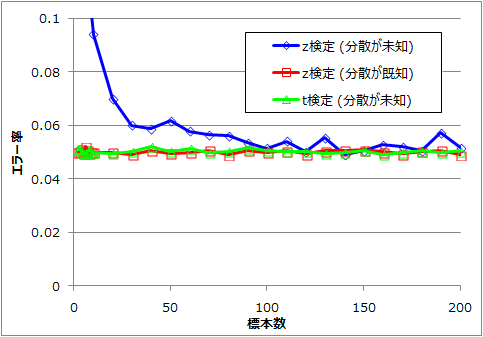
やっていることは単純で、N(0, 1)の正規分布のデータ列を生成して、各検定で有意水準5%の領域に入る確率をチェック。確率は5%になるはずです。
結果 †
思った以上にt検定が強い。というか検定はt検定で良いのでは...と思ってしまう。